La formation pédagogique

Cette page est principalement destinée aux formateurs. Vous êtes conseiller pédagogique, maître formateur, référent mathématique de circonscription, ... et vous souhaitez engager un cycle de formation sur les fractions et les nombres décimaux ? Nous vous proposons de partager avec vous les ressources que nous avons construites depuis des années. Tous les documents pédagogiques accessibles sur le site sont en licence creative commons. Ci-dessous, nous mettons à votre disposition quelques éléments pour une première compréhension des enjeux de formation. Pour tout renseignement complémentaire, nous vous proposons de prendre un premier contact avec vous de la façon qui vous conviendra : mail, téléphone, visio-conférence,...
Formation de formateurs
Nous sommes intervenus en formation de formateurs dans de nombreux espaces, tels que l'Institut Français de l'Education ou le Centre Alain Savary à l'ENS de Lyon, mais aussi dans dans des colloques (IREM, COPIRELEM, L'école du 21e siècle). Comme nous l'avons fait à plusieurs reprises dans les académies de Bourgogne Franche-Comté ou Rhône Alpes, nous pouvons intervenir dans votre académie pour organiser une journée de formation de formateurs avec pour double objectif de vous faire découvrir nos situations didactico-pédagogiques et d'envisager les modalités d'accompagnement des enseignants lors de formations pédagogiques ou de contellations.
En tant que formateurs, notre proposition est d’accompagner les enseignants dans la durée à l’aide de matériels extraits de la classe. Nous ramenons le réel en formation à l'aide de nombreuses vidéos d'élèves et d'enseignants. Cela nous permet de développer les compétences pédagogiques et didactiques des enseignants. Les vidéos que nous utilisons dans notre intervention constituent une première base que nous pouvons partager avec les formateurs.
N'hésitez pas à nous contacter pour envisager avec nous les contours possibles de cette intervention.
Analyse de l'activité
Notre façon de penser la formation pédagogique en circonscription a été documentée par le Centre Alain Savary - Institut Français de l'Education. C'est le fruit d'une longue collaboration entre le CAS et nos équipes de circonscription. Pour accéder aux ressources qu'ils mettent à disposition, cliquer sur l'icône ci-contre.
Cadre didactique
Notre scénario pédagogique sur l'enseignement des fractions s'appuie sur la Théorie
des Situations Didactiques (TSD) de Guy Brousseau. Il propose des situations d'action adossées à du
matériel (bandes de papier ou disques en plastique) visant l'apprentissage de connaissances
mathématiques relatives aux fractions simples dans un contexte de partie / tout. Toutefois,
l'activité des élèves et la manipulation ne constituent pas des conditions suffisantes à la
construction des apprentissages.
Si l'élève agit sans but, il manipule les bandes ou les fractions de disque sans enjeu, "l'action
n'est pas finalisée. Par conséquent, il n'élabore pas de stratégies en dialoguant avec les éléments
du contexte". C'est la raison pour laquelle, nous avons fait le choix de contraindre son action par
des variables didactiques, indispensables à la construction des connaissances mathématiques, en cela
qu'elles imposent aux élèves d'anticiper et de donner un but à l'usage du matériel. Toutes les
situations sont auto-validantes, l'élève peut examiner si la stratégie engagée permet de répondre à
la consigne, et d'engager une nouvelle démarche si tel n'est pas le cas.
Le scénario propose par ailleurs des situations de formulation qui ont pour but d'engager les élèves
vers un niveau d'abstraction supérieur à celui des situations d'action. Ces situations de
formulation doivent amener l'élève à transporter la connaissance mathématique pour lui-même, pour un
pair ou encore pour le groupe classe. Dans ce but, nous empêchons l'élève d'agir directement sur le
matériel, en éloignant son action dans l'espace ou dans le temps.
Nos situations présentent des caractéristiques communes : un matériel simple, un type de tâche récurrent, une mise à distance des objets pour forcer la représentation mentale, une auto-validation par l'élève.
Adossé aux travaux de G. Brousseau et J. Briand, notre cadre didactique suppose :
- Pour l'élève
- Prendre en charge l'activité dans des situations auto-validantes.
- Accroître le temps et le rôle de la manipulation d'objets.
- Construire et mobiliser une représentation mentale des fractions étudiées.
- Utiliser le matériel comme aide à la représentation ou après anticipation de la réponse, en appui à une démarche ou pour valider le résultat.
- Exercer un contrôle pragmatique lors de l'élaboration d'une démarche, de la production d'une réponse.
- Communiquer une réponse, une démarche, pour soi-même, pour autrui, pour le groupe classe.
- Mesurer ou estimer la longueur d'une bande ou d'un segment, d'un disque, de surfaces rectangulaires à l'aide d'une unité de référence, selon des variables de mise à distance ou de disparition du matériel.
- Pour l'enseignant
- Consacrer un temps important à des activités de construction des notions et diminuer le temps d'exercisation des compétences.
- Prévoir des temps d'oral avec les élèves, le groupe classe pour mettre du langage sur les démarches, la construction des savoirs, leur institutionnalisation.
- Adopter les gestes professionnels et les postures indispensables à la mise en œuvre d'un enseignement systématique, c'est à dire explicite et structuré des fractions et des nombres décimaux.
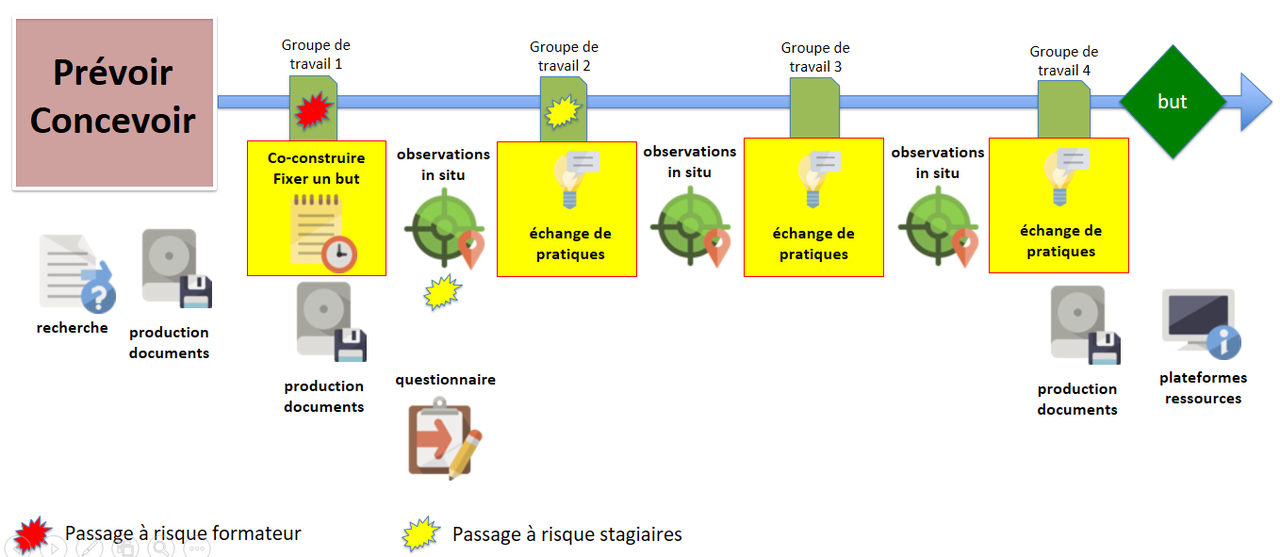
Ramener le réel en formation
Depuis maintenant quatre années, de nombreux enseignants mettent en oeuvre le scénario pédagogique
Klásma dans leurs classes de cycle 3. Dans les deux circonscriptions où il a été développé, le
scénario est présent dans l'ensemble des écoles, garantissant ainsi une congruence de pratiques très
bénéfique, d'abord pour les élèves, mais aussi pour les équipes pédagogiques. C'est le résultat du
long travail de notre collectif de conseillers pédagogiques et de professeurs des écoles. Nous
concevons nos formations dans une logique pluri-annuelle afin de donner le temps aux enseignants de
s'approprier le scénario, d'expérimenter, de questionner... A la lumière des observations menées en
classe et grâce aux échanges avec les collègues enseignants engagés dans des groupes de recherche /
action, le collectif précise et améliore la proposition pédagogique pour s'assurer de son
acceptabilité et la rendre plus efficiente.
Le travail est ensuite présenté en formation pédagogique à l'ensemble des enseignants qui disposent
de plusieurs années de formation pour mettre en oeuvre et discuter des obstacles rencontrés et des
effets obdservés. A l'aide de vidéos montrant l'activité des élèves ou/et celle des enseignants,
nous ramenons le réel de la classe en formation et les enseignants des groupes de travail
interviennent pour présenter leur travail, les effets sur leurs propres pratiques et sur les
compétences de leurs élèves.
| Klásma Situation 1 | Fabriquer une bande de même longueur à l’aide d’une bande unité | ||
|
Objectifs : Construire le concept de fraction. Construire les notions de moitié, quart et huitième à partir du pliage de la bande unité en deux, quatre et huit parties égales. Tâche de l'élève : Les élèves doivent reproduire une bande de leur choix, grâce à une bande unité (uniquement). La bande découpée devra être exactement de la même longueur que la bande choisie. Pour fabriquer la bande de même mesure, les élèves disposent d’une seconde bande unité (identique à la première) et de bandes blanches à découper (placées dans une enveloppe ou mises à disposition en fond de classe). L'élève doit effectuer la mesure de la bande qu'il a choisie à l'aide d'une bande unité puis reproduire à distance une bande de même longueur avec une seconde bande unité (identique à la première). Une fois le découpage fait, il revient à sa place pour vérifier et recommencer ou passer à une autre bande. Dans la vidéo, les déplacements de l'élève de l'espace de mesure à l'espace de découpe sont matérialisés par les fondus en noir. Analyse de la vidéo : L'élève a été momentanément sorti de la classe pour les besoins de la vidéo. Pour cet élève de CM1, c'est la première fois qu'il réalise la tâche. Le cadre didactique est celui de la Théorie des Situations Didactiques (TSD). Les élèves sont placés dans une situation autovalidante. Ainsi, l'enseignant déchargé de la validation peut se consacrer à l'observation des procédures et à l'étayage langagier nécessaire à la construction du concept de fraction. Le dispositif doit permettre de répéter à plusieurs reprises des expériences de reproduction de bandes. Il doit aussi permettre aux élèves de travailler à leur rythme. Ce qui présente l'avantage d'intégrer une différenciation pédagogique sans surcharge de préparation pour l'enseignant. Ce que l'on peut dire de cet élève : Il met en oeuvre une procédure efficiente de pliage de la bande en 2 parties égales. Il est assez rare d'observer cela chez un élève dès les premières tentatives. Par contre, il manque de précision et doit donc recommencer. Pour autant, il garde confiance en sa procédure et sa deuxième tentative est fructueuse. Pour la plupart des élèves, il faudra de nombreux essais, parfois une séance complète avant de comprendre qu'il faut plier la bande, et comment le faire. Il faut leur laisser le temps de le faire pour qu'ils puissent construire le concept de fraction de l'unité. L'observation des camarades ainsi que les échanges peuvent permettre de débloquer des situations. Les temps collectifs sont très importants pour institutionnaliser les procédures et les savoirs relatifs à cet activité. |
|||
| Klásma Situation 2 | Comparer plusieurs longueurs de bandes pour reconstituer des paires de même longueur | ||
|
Objectif : Comparer des fractions et construire des égalités élémentaires Tâche de l'élève : Les élèves mesurent les bandes placées dans une enveloppe pour retrouver celles qui sont de même longueur. Ils ne peuvent sortir et mesurer qu'une seule bande à la fois. Chaque bande mesurée est placée dans une seconde enveloppe avant de passer à la bande suivante. La valeur de chaque mesure est conservée. Une fois les mesures effectuées, les élèves retrouvent les paires puis vérifient en sortant toutes les bandes de l'enveloppe. Analyse de la vidéo : Après avoir appris à mesurer des bandes lors de la première situation, les élèves sont placés dans une situation de comparaison. Les élèves travaillent en binômes. Au moment de la vidéo, ils ont déjà écrit les mesures. On peut observer ici le rôle primordial du matériel mis à leur disposition : il est un outil indispensable pour aider les élèves à construire les concepts progressivement. La manipulation permet de chercher, de contrôler, de valider. Un des deux élèves se réfère sans cesse aux bandes de papier pour échanger avec sa voisine qui a déjà atteint un niveau d'abstraction plus avancé et travaille mentalement. C'est grâce à ce support qu'ils peuvent communiquer et discuter. |
|||
| Klásma Situation 4 | Reconstituer l’unité à partir de fractions de l’unité différentes. | ||
|
Objectifs : S’approprier le matériel. Identifier les fractions de l’unité par reconstitution de l’unité. Construire une expérience manipulatoire et mentale des fractions. Tâche de l'élève : Les élèves doivent intervertir des pièces entre les disques pour trouver des fractions égales. Pour ce faire, ils vont échanger des pièces entre deux disques à la fois. Analyse de la vidéo : Tout d'abord, on comprend bien l'intérêt de l'usage du matériel. Les élèves et l'enseignant y font référence en permanence. Sans cet appui, les échanges ne pourraient se conduire avec une telle efficience. On observe ici le rôle de l'étayage de l'enseignant pendant l'activité des élèves. Les échanges entre élèves sont tout à fait intéressants, mais on voit qu'ils ont besoin que l'enseignant vienne repréciser la consigne afin d'orienter l'activité et de permettre aux élèves de conscientiser. Sans cet apport, les élèves pourraient s'enfermer dans une activité type "puzzle", renforcée par l'usage du matériel (car la manipulation ne peut pas suffire). Lors de ces moments, l'enseignant observe les procédures et accompagne les élèves dans leurs apprentissages. A discuter et expliciter avec les enseignants : Si au début de l'activité, la consigne explicite clairement la tâche de l'élève et l'objectif puis que pendant l'activité, l'enseignant permet de conscientiser par un travail langagier, les temps d'institutionnalisation sont alors beaucoup plus faciles à mener avec des élèves qui ne se concentrent pas uniquement sur la tâche. Au lieu de se limiter à raconter ce qu'ils ont fait, ils sont alors capables d'expliciter ce qu'ils ont appris. |
|||

